this post was submitted on 13 Oct 2024
472 points (98.0% liked)
Asklemmy
43919 readers
1022 users here now
A loosely moderated place to ask open-ended questions
Search asklemmy ๐
If your post meets the following criteria, it's welcome here!
- Open-ended question
- Not offensive: at this point, we do not have the bandwidth to moderate overtly political discussions. Assume best intent and be excellent to each other.
- Not regarding using or support for Lemmy: context, see the list of support communities and tools for finding communities below
- Not ad nauseam inducing: please make sure it is a question that would be new to most members
- An actual topic of discussion
Looking for support?
Looking for a community?
~Icon~ ~by~ ~@Double_A@discuss.tchncs.de~
founded 5 years ago
MODERATORS
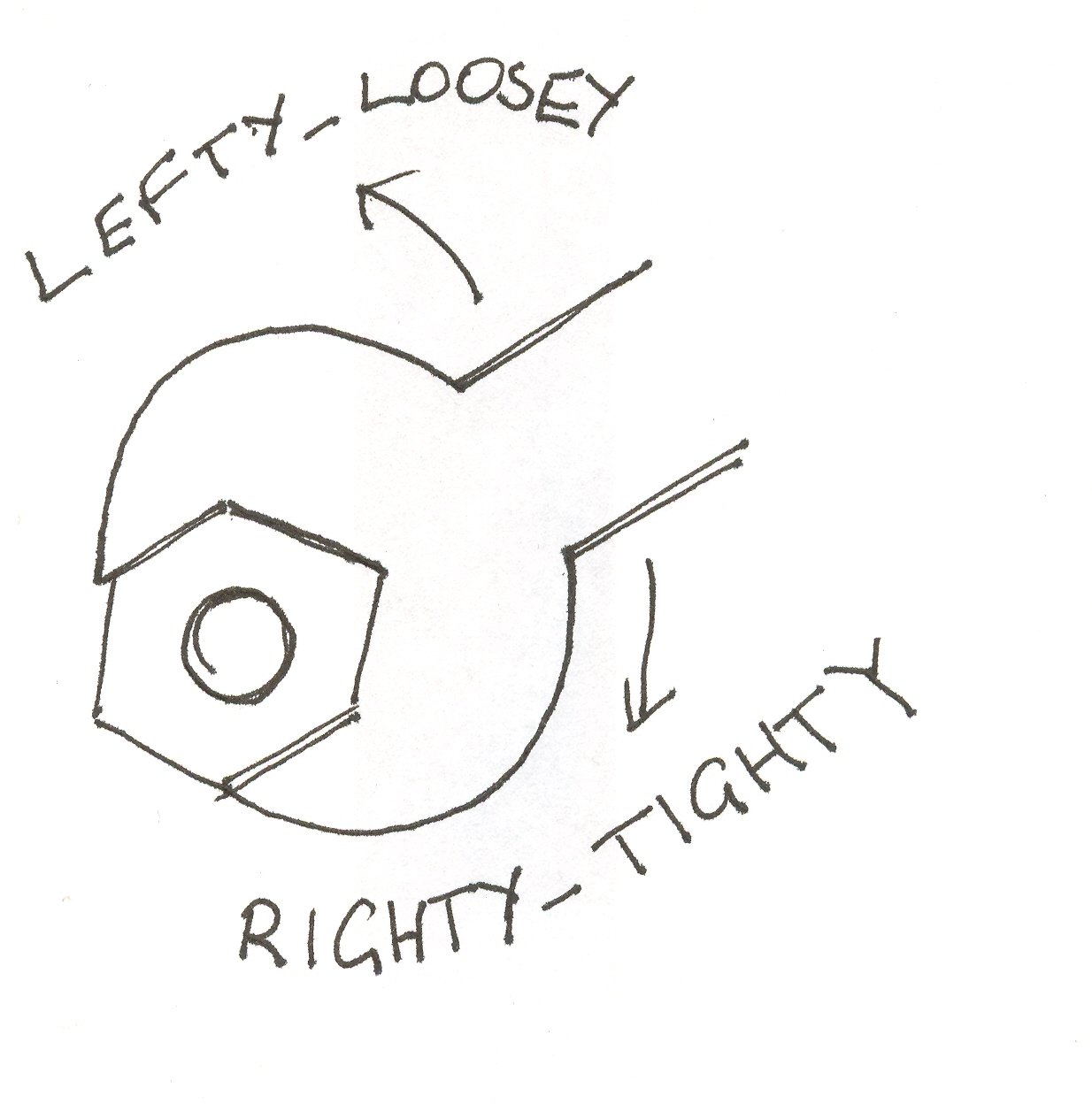
So you're explaining rotation, in terms of a smaller imaginary rotation, which engages with imaginary traction wheels, which engage with the work to be turned?
If that works for you, great, but it is complicated.
No im trying to illustrate the parallels between how you turn the wheel, how the car turns in response to that , and how they are all related. You turn left you will make the exact same rotational movement, with both the vehicle, and the steering wheel.
It's as simple as, "What direction do you turn the wheel to make the car go left?" I just stacked on top "and also it makes the car itself do that same exact circular movement" so you don't just dismiss this as some kind of arbitrary convention.
Oh, I see.
Car steering wheels work that way because of the convention. Change the side that the steering column's pinion meets the rack and the wheel would work the opposite way. From the mathematical perspective, there's two ways to continuously map an arc of the steering wheel to an arc of the wheels, and since they aren't in the same plane neither is "wrong".
i know you can make the wheel work the opposite way, jesus christ. the circle motion the path of the car makes when you turn left is the same as when you turn the wheel to the conventional left. imagine, instead you steered "left" by a joystick. the car would still draw the same circular path the same fucking way, because turning left makes an anticlockwise circle, every time, in every situation.
Ah, so the car isn't even important. You're one of the people imagining standing on the screw. As long as you have a convention about which way is "up" on it, that does work.
You have to have a convention about Up to usefully describe a rotational direction at all. I don't see how that's relevant. Left implies an Up.
Yes, it's true, you do. Left doesn't really imply an up so much as it comes as a package with one, though. I'm not OP, but historically I had the same issue. I just didn't automatically jump to "in is down, and I'm on the rim", and instead was thinking about my actual physical left and right at that moment.
You don't really need to visualize yourself on the rim, either. Just turn left in any context and you will trace the path of an anticlockwise circle. It's really more about establishing why there's a link between left and anticlockwise. Picture and remember whatever works best for you, I'm just annoyed by the people stubbornly insisting the link between them doesn't make perfect sense.
One of them is "wrong" and would kill many people