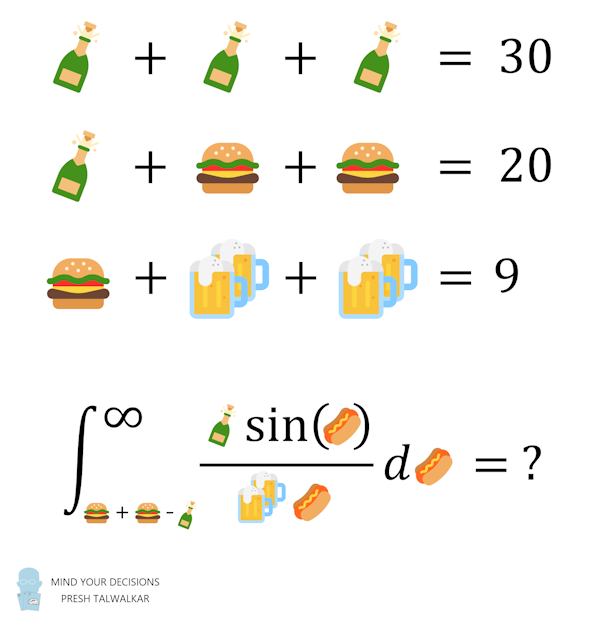math
269 readers
2 users here now
Interesting news and discussion centered around Mathematics
founded 1 year ago
MODERATORS
1
2
3
4
5
6
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22